图的路径生成

• 加权图——提高或降低某些边的权重
• 图的储存结构--邻接矩阵,邻接表,十字链表
• 最小生成树---prim算法,kruskal算法
• 最短路径--dijkstra算法,floyed算法,bellman-ford算法

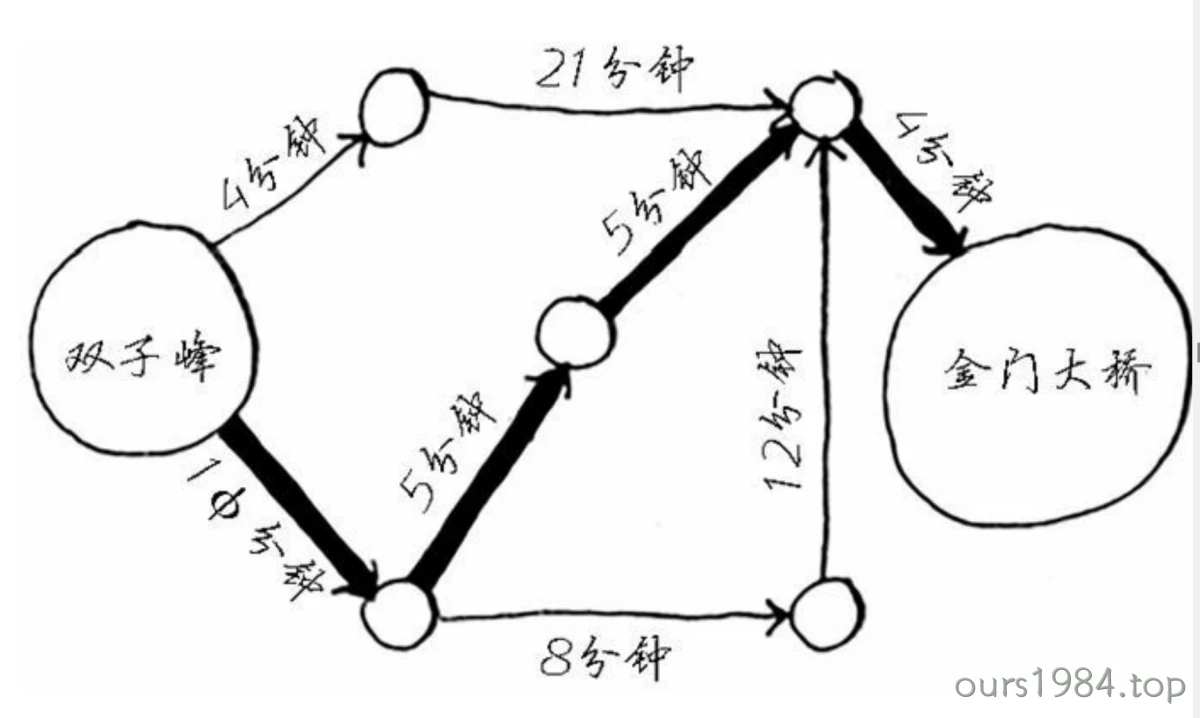
加权图

图的储存结构

邻接矩阵

Adjacency Matrix储存方式是用两个数组来表示图.一个一维数组储存顶点信息,一个二维数组(邻接矩阵)储存图中的边弧信息.

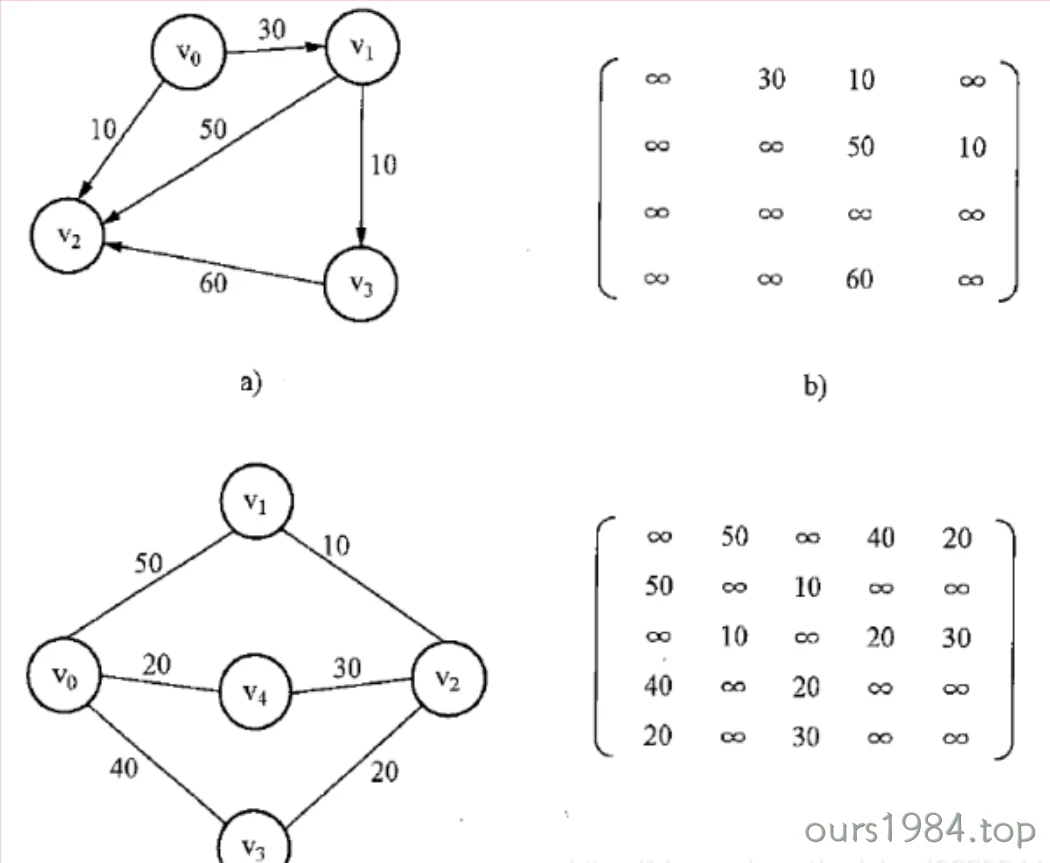
设G=(V,E)是n个顶点的图，则G的邻接矩阵用n阶方阵G表示，若(Vi ,Vj )或< Vi ,Vj > 属于 E(G)，则G[i][j]为边或弧的权Wij，否则Vi与Vj间无边或弧，用 ∞ 表示。

Void CreatGraph(Graph *g){ 
    int i,j,n,e,w;
    char ch;
    scanf("%d %d",&n,&e);
    g->vexnum=n;
    g->arcnum=e;
    for (i=0;i<g->vexnum;i++){
        scanf("%c",&ch);
        g->vexs[i]=ch;
    };
    for (i=0;i<g->vexnum;i++){
        for (j=0;j<g->vexnum;j++){
            g->arcs[i][j]=MAX_INT
        }
    };
    for (k=0;k<g->arcnum;k++){
        scanf("%d %d %d",&i, &j,&w);
        g->arcs[i][j]=w;
        g->arcs[j][i]=w;
    }
}

邻接表

考虑到邻接矩阵的空间蓝付费问题,邻接表是顺序存储与链式存储相结合的存储方法。

在邻接表中，对图中每个顶点建立一个单链表，每个单链表中链接图中与顶点相邻接的所有顶点。

邻接表中的每个单链表均有一个表头结点，表头结点均含有两个域 ，一个是 vertex，用于存放当前顶点的信息，另一个是firstarc，用于指向邻接表中的第一个结点。

邻接表中的每个单链表含有不等个数的表结点，表结点含有两或三个域，一个是adjvex，存放与顶点相邻接顶点的序号，另一个是nextarc，指向该顶点的下一个邻接点，带权图表结点的形式还会多一个weight表示权重

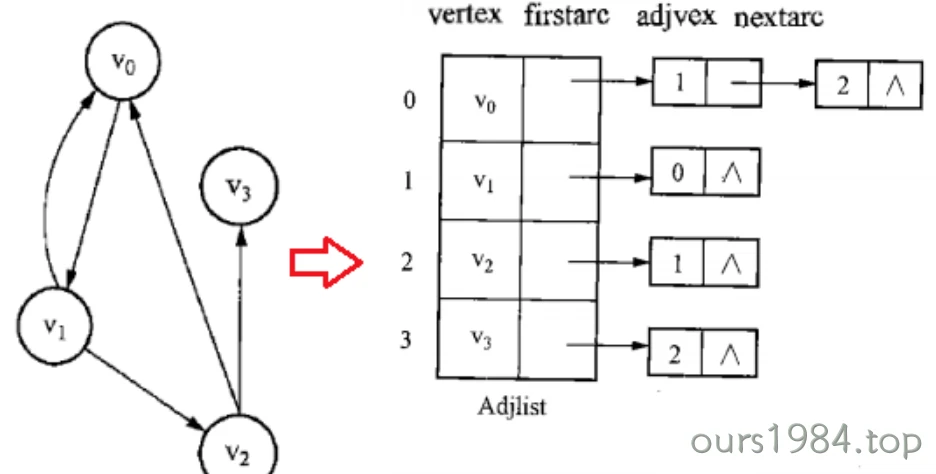
(1). n个顶点、e条边的无向图，则其邻接表的表头结点数为n， 链表结点总数为2e；

(2). 对于无向图，第i个链表的结点数为顶点Vi的度；对于有向图，第i个链表的结点数为顶点Vi的出度；

(3). 在边稀疏时，邻接表比邻接矩阵省单元；

(4). 邻接表表示在检测边数方面比邻接矩阵表示效率要高。

十字链表

在有向图的邻接表中,边链表表示了节点的出度,如果要计算入度,则比较麻烦

一般的做法是,同时简历一个逆邻接表,边链表为接待你的入度.需要同时维护两张边表

更通用的做法是十字链表,在变结构中同时储存入点/出点/入边/出边,这样查询就比较方便了

struct EdgeNode
{
    int inId;
    int outId;

    EdgeNode *in=nullptr;
    EdgeNode *out=nullptr;

    EdgeData data;
};

struct VertexNode
{
    VertexData data;
    bool init = false;
    EdgeNode *firstIn = nullptr;
    EdgeNode *firstOut = nullptr;
};

struct graph
{
    int numEdges=0;
    std::vector<bool> flags;
    std::queue<int> queflag;
    std::vector<VertexNode> nodes;
}

最小生成树

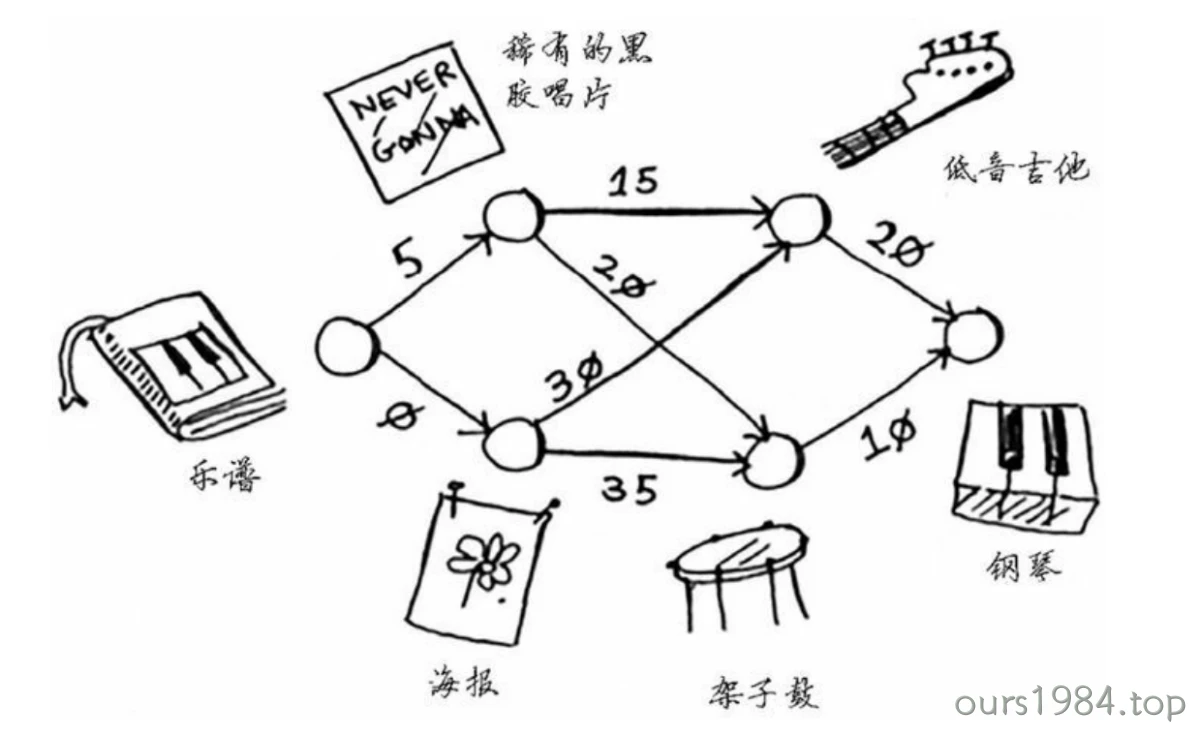
prim算法

普里姆算法查找最小生成树的过程，采用了贪心算法的思想。对于包含 N 个顶点的连通网，普里姆算法每次从连通网中找出一个权值最小的边，这样的操作重复 N-1 次，由 N-1 条权值最小的边组成的生成树就是最小生成树。

那么，如何找出 N-1 条权值最小的边呢？普里姆算法的实现思路是：

1. 将连通网中的所有顶点分为两类（假设为 A 类和 B 类）。初始状态下，所有顶点位于 B 类；
2. 选择任意一个顶点，将其从 B 类移动到 A 类；
3. 从 B 类的所有顶点出发，找出一条连接着 A 类中的某个顶点且权值最小的边，将此边连接着的 A 类中的顶点移动到 B 类；
4. 重复执行第 3 步，直至 B 类中的所有顶点全部移动到 A 类，恰好可以找到 N-1 条边。

#include<stdio.h>
#define V 6    // 记录图中顶点的个数
typedef enum { false, true } bool;
//查找权值最小的、尚未被选择的顶点，key 数组记录了各顶点之间的权值数据，visited数组记录着各个顶点是否已经被选择的信息
int min_Key(int key[], bool visited[])
{
    int min = 2147483647, min_index;  //遍历 key 数组使用，min 记录最小的权值，min_index 记录最小权值关联的顶点
    //遍历 key 数组
    for (int v = 0; v < V; v++) {
        //如果当前顶点为被选择，且对应的权值小于 min 值
        if (visited[v] == false && key[v] < min) {
            //更新  min 的值并记录该顶点的位置
            min = key[v];
            min_index = v;
        }
    }
    //返回最小权值的顶点的位置
    return min_index;
}

//根据用户提供了图的信息（存储在 cost 数组中），寻找最小生成树
void find_MST(int cost[V][V])
{    //key 数组用于记录 B 类顶点到 A 类顶点的权值
    //parent 数组用于记录最小生成树中各个顶点父节点的位置，便于最终生成最小生成树
    //visited 数组用于记录各个顶点属于 A 类还是 B 类
    int parent[V], key[V];
    bool visited[V];
    // 初始化 3 个数组
    for (int i = 0; i < V; i++) {
        key[i] = 2147483647;    // 将 key 数组各个位置设置为无限大的数
        visited[i] = false;     // 所有的顶点全部属于 B 类
        parent[i] = -1;         // 所有顶点都没有父节点
    }
    // 选择 key 数组中第一个顶点，开始寻找最小生成树
    key[0] = 0;  // 该顶点对应的权值设为 0
    parent[0] = -1; // 该顶点没有父节点
    // 对于 V 个顶点的图，最需选择 V-1 条路径，即可构成最小生成树
    for (int x = 0; x < V - 1; x++)
    {
        // 从 key 数组中找到权值最小的顶点所在的位置
        int u = min_Key(key, visited);
        // 该顶点划分到 A 类
        visited[u] = true;
        // 由于新顶点加入 A 类，因此需要更新 key 数组中的数据
        for (int v = 0; v < V; v++)
        {
            // 如果类 B 中存在到下标为 u 的顶点的权值比 key 数组中记录的权值还小，表明新顶点的加入，使得类 B 到类 A 顶点的权值有了更好的选择
            if (cost[u][v] != 0 && visited[v] == false && cost[u][v] < key[v])
            {
                // 更新 parent 数组记录的各个顶点父节点的信息
                parent[v] = u;
                // 更新 key 数组
                key[v] = cost[u][v];
            }
        }
    }
}

由算法代码可知,时间复杂度为\(O(n^2)\)

kruskal算法

将连通网中所有的边按照权值大小做升序排序，从权值最小的边开始选择，只要此边不和已选择的边一起构成环路，就可以选择它组成最小生成树。对于 N 个顶点的连通网，挑选出 N-1 条符合条件的边，这些边组成的生成树就是最小生成树。

假设连通网N = ( V , E ) N=(V,E)N=(V,E)，将N NN中的边按权值从小到大的顺序排列。

1. 初始状态为只有n nn个顶点而无边的非连通图T = ( V , { } ) T=(V,{})T=(V,{})，图中每个顶点自成一个连通分量。
2. 在E EE中选择权值最小的边，若该边依附的顶点落在T TT中不同的连通分量上（即不形成回路），则将此边将入到T TT中，否则舍去此边而选择下一条权值最小的边。
3. 重复2，直到T TT中所有的顶点都在同一连通分量上为止。

这个算法的构造过程十分简洁明了，那么为什么这样的构造过程能否形成最小生成树呢？我们来看第二个步骤，因为我们选取的边的顶点是不同的连通分量，且边权值是最小的，所以我们保证加入的边都不使得T TT有回路，且权值也最小。这样最后当所有的连通分量都相同时，即所有的顶点都在生成树中被连接成功了，我们构造成的树也就是最小生成树了。

#define N 9   // 图中边的数量
#define P 6   // 图中顶点的数量
//构建表示边的结构体
struct edge {
    //一条边有 2 个顶点
    int initial;
    int end;
    //边的权值
    int weight;
};
//qsort排序函数中使用，使edges结构体中的边按照权值大小升序排序
int cmp(const void* a, const void* b) {
    return  ((struct edge*)a)->weight - ((struct edge*)b)->weight;
}
//克鲁斯卡尔算法寻找最小生成树，edges 存储用户输入的图的各个边，minTree 用于记录组成最小生成树的各个边
void kruskal_MinTree(struct edge edges[], struct edge minTree[]) {
    int i, initial, end, elem, k;
    //每个顶点配置一个标记值
    int assists[P];
    int num = 0;
    //初始状态下，每个顶点的标记都不相同
    for (i = 0; i < P; i++) {
        assists[i] = i;
    }
    //根据权值，对所有边进行升序排序
    qsort(edges, N, sizeof(edges[0]), cmp);
    //遍历所有的边
    for (i = 0; i < N; i++) {
        //找到当前边的两个顶点在 assists 数组中的位置下标
        initial = edges[i].initial - 1;
        end = edges[i].end - 1;
        //如果顶点位置存在且顶点的标记不同，说明不在一个集合中，不会产生回路
        if (assists[initial] != assists[end]) {
            //记录该边，作为最小生成树的组成部分
            minTree[num] = edges[i];
            //计数+1
            num++;
            elem = assists[end];
            //将新加入生成树的顶点标记全部改为一样的
            for (k = 0; k < P; k++) {
                if (assists[k] == elem) {
                    assists[k] = assists[initial];
                }
            }
            //如果选择的边的数量和顶点数相差1，证明最小生成树已经形成，退出循环
            if (num == P - 1) {
                break;
            }
        }
    }
}

Find时间复杂读为\(O(\lg e)\),外面for循环e次,所以kruskal时间复杂度为\(O(e\lg e)\)

小结

如果你在哪儿卡住了，可以到这里查看源码。