移动立方体(Marching Cubes,MC)算法
移动立方体(Marching Cubes)算法是面绘制算法中的经典算法,它是W.Lorensen等人于1987年提出的体素级重建算法,也被称为“等值面提取”(Isosurface Extration)算法。
算法主要的思想
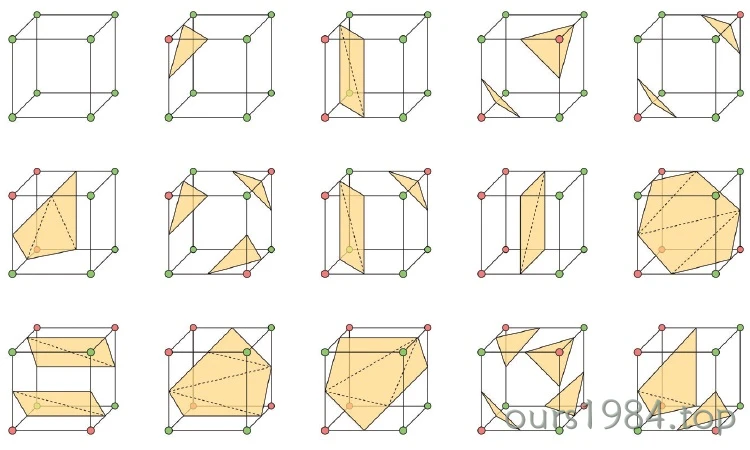
在三维离散数据场中通过线性插值来逼近等值面。具体如下:三维离散数据场中每个栅格单元作为一个体素,体素的每个顶点都存在对应的标量值。如果体素顶点上的值大于或等于等值面值,则定义该顶点位于等值面之外,标记为“0”;而如果体素顶点上的值小于等值面值,则定义该顶点位于等值面之内,标记为“1”。由于每个体素单元有8个顶点,那么共存在2^8 = 256种情形,下图是Marching Cubes算法的15种基本情形,其他241种情形可以通过这15种基本情形的旋转、映射等方式实现。
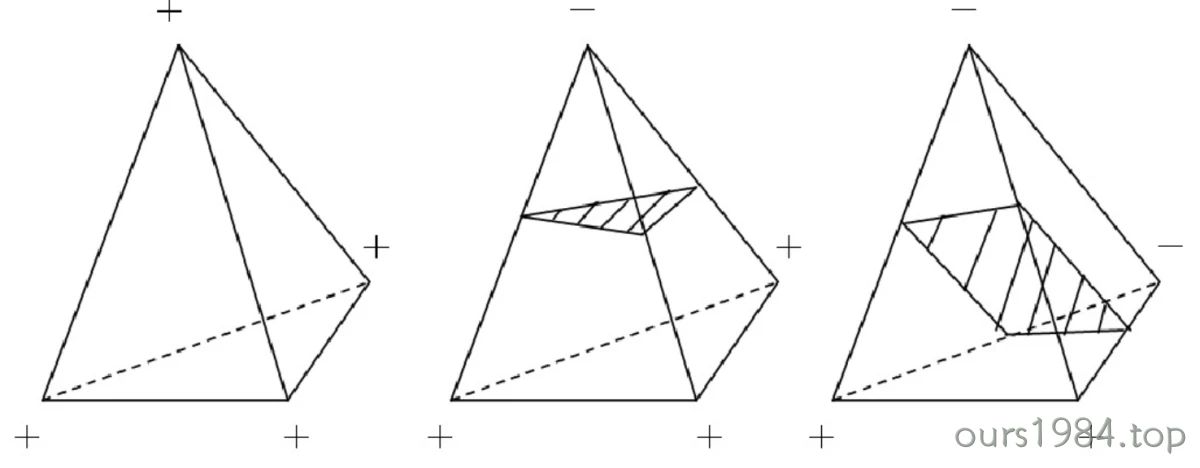
对于四面体来说,则只有三种情况,如下图。其他立方体,如楔形体/金字塔,由三角面和四边面组合而成,也可以列出相应多种情况。二阶单元连接方式不变,可以先划分为多个一阶单元,再按一阶方式计算。或者直接忽略掉二阶顶点按一阶方式计算(损失信息)
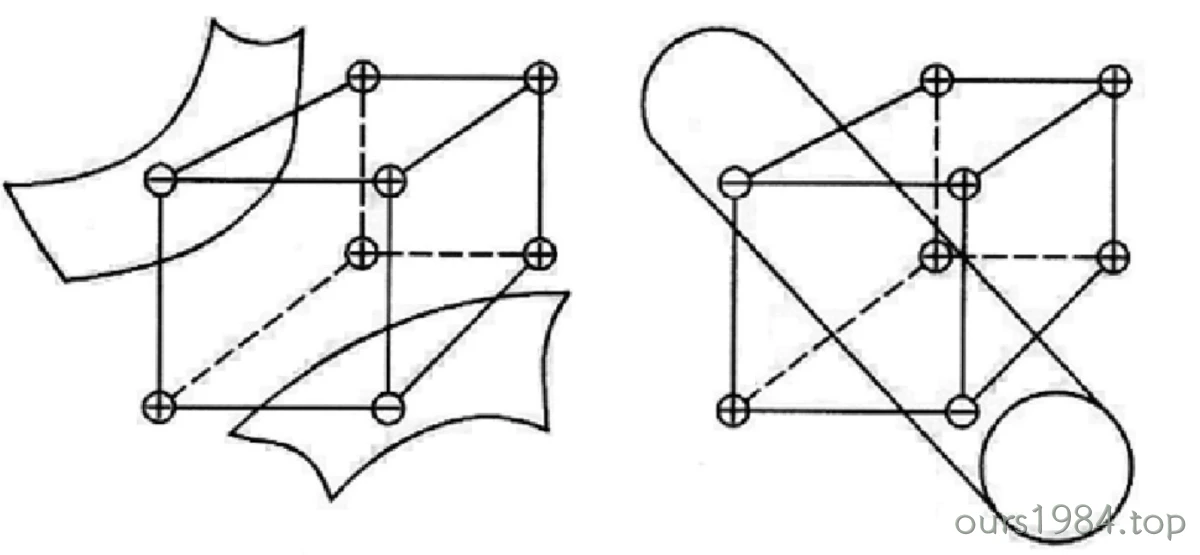
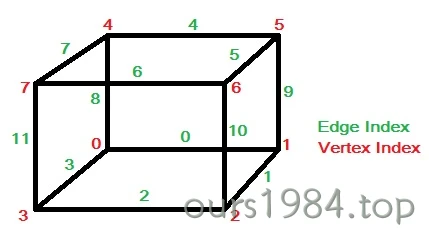
每个体素单元上顶点和边的索引规则如下图左所示,假如体素下方的顶点3的值小于等值面值,其他顶点上的值都大于等值面值(如下图右所示),那么我们可以生成一个与体素边2,3,11相交的三角面片,而三角面片顶点的具体位置则需要根据等值面值和边顶点3-2,3-0,3-7的值线性插值计算得到。
对于与等值面存在交点的体素边,交点坐标用P表示,P1、P2代表边上两个端点的坐标,V1、V2代表这两个端点上的值,V代表等值面值,那么交点坐标的计算公式如下:
\[P = P1 + (V – V1)·(P2 – P1)/(V2 – V1)\]
算法步骤
1.确定包含等值面的体元(线段树加速)
2.确定体元对应的等值面片模式(查表)
3.计算等值面与体元边界交点连接成三角形(顶点去重)
4.计算等值面法向(考虑共用顶点情况)
存在问题
1.只通过体元边上的点,构造出来的三角面不够精确,没有包含体/面信息。无解。
2.连接方式二意性。解决方式:对二义性情况,增加采样点,增加case,消除二义性