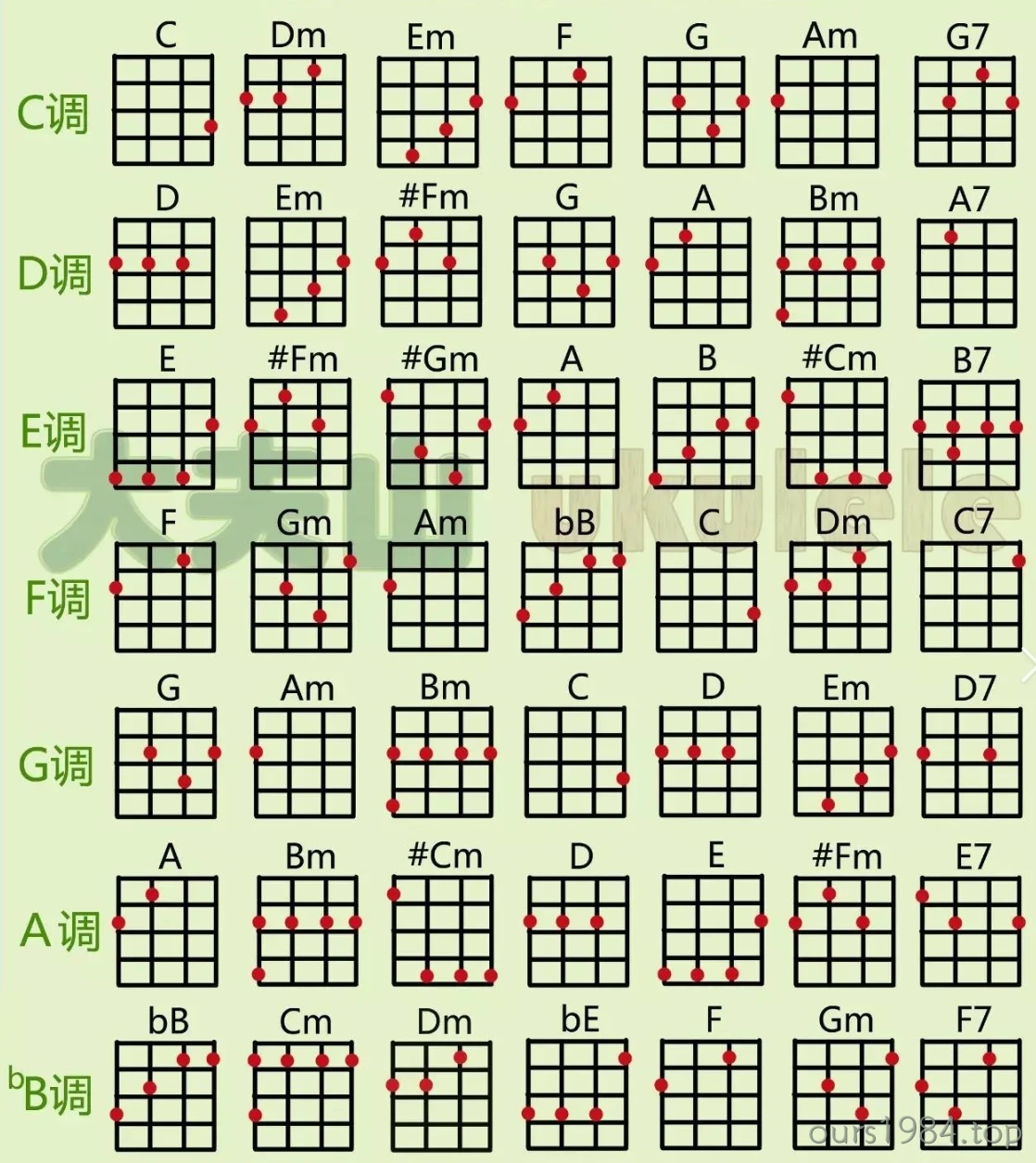
乐理入门之调式和弦级数

我们先从这个问题开始：从连续的频率谱中选择几个不同频率的音，如何选择才能让它们放在一起听上去和谐悦耳？

这个问题被古往今来无数乐理大师研究过了，得到的答案是：两个音的频率之比越接近简单的整数比，它们听起来就越和谐。

楔子

给频率为220Hz的音起一个名字叫做A。

最简单的整数比是「1:2」，让音A对应比例中的1，那么比例中的2对应了频率为440Hz的音，不妨叫这个音为a。根据上面的规则，A和a应该是非常和谐的两个音。

事实上确实如此，a的频率是A的两倍，这是各种两个音的组合里面听起来最完美和谐的一种。A和a之间的差别叫做纯八度，听起来就很纯对吧。

再找一个简单的整数比「2:3」，同样让音A对应这里的2，那么比例中的3对应了频率为330Hz的音，把这个音叫做E。确实，A和E也是相当和谐的两个音，同时听到这两个音不会有违和感。这两个音之间的差别叫做纯五度。

类似地，以音A=220Hz为基础，套用整数比「3:4」，得到音D=293Hz，这两个音也比较和谐，它们是纯四度。

当然，音程名字里面带有「纯」不是它们和谐的本质原因，「大三度」「小六度」和谐程度也还不错，它们对应的比例则（大约是）「4:5」和「3:5」。

用这几个音A、D、E、a已经能创作一些不错的旋律了，哪怕只是将它们随便排列一下，听上去也能感觉到它们仿佛天生就是一套的。

但如果随便找个别的频率比如230Hz，把它加入上面那几个音组成的旋律，就会觉得很违和，仿佛有奇怪的东西混进来了。

显然，230Hz的音与我们的A=220Hz频率之比是一个不那么“简单”的比例「22:23」，我们不禁想问，「简单整数比」为何会具有如此魔力，能让两个音听上去和谐悦耳？

单纯在乐理的领域很难触及到这个问题的深层答案。我猜它甚至大概率和人耳的遗传性质没什么关系，因为这实际上是一个物理问题……

原理

一个物体要发出持续稳定的声波，需要这个声波在物体内形成「驻波」。不是任何声波都能在物体内形成驻波，它需要这样的条件：

在声波传播的方向上，物体的尺寸是声波半波长的整数倍。物体的尺寸限制了声波能够行进的范围。

• 当声波行进到物体边界时发生反射，回波与原波之间发生干涉叠加。回波走到物体的另一头，又再次发生反射，产生回波的回波，一直套娃下去……
• 当这个范围（物体的尺寸）是半波长整数倍时，这些声波叠加的最终结果，将得到一个持续稳定的「驻波」。

驻波的振幅、相位是有规律的，它能够向外辐射频率稳定的声波，传到人耳中就成了特定音调的声音。无法形成驻波的频率，叠加以后会自我抵消、耗散，向外辐射的也是不稳定的杂音。

敲击一个物体，就是在这个物体上激发各个频率的声波。我们从发出的声音中辨识出来的音调，则是这些频率里面能够在物体内形成驻波的那一部分。

驻波实验

有一根长度为4的弦，我们在弦的中点位置激发一个波长为1的波。

它的半波长是0.5，符合「物体的尺寸是半波长整数倍」

红色是原波，蓝色和绿色分别是原波碰到左、右边界后产生的反射波，玫红色是叠加以后的波：

可以看到玫红色的波只在原地上下扭动，没有沿着弦左右移动，这就是驻扎在原地的「驻波」。驻波振幅最大的「波腹」与振幅最小的「波节」位置是固定的，而且振幅非常协调一致。

杂波实验

如果换一根长度为\(2\sqrt{3}\)的弦，它不是半波长的整数倍，得到的叠加波会变得杂乱无章。为了更清楚地看到叠加以后的波，咱们把它突出显示：

这时候叠加的波不再有稳定的波腹和波节了，不再是驻波。上图还没有画出回波的回波，要是把它们也放进去，最终叠加的波会更加混乱。

泛音列

们已经知道形成驻波的条件是「物体的尺寸是半波长整数倍」，那么，对于一个特定的发声物体，哪些频率能够形成驻波呢？

通过驻波条件,数学运算后,我们不难得出结论,驻波的频率是某一个基准频率的整数倍,它不是一个,它是一系列的

c为物体上的声速,l为物体尺寸,可以得出

频率最低的（ c/2l ），叫做「第一泛音」或者「基音」，它是这一众泛音里面响度（振幅）最大的一个

频率为基音2倍的（ 2⋅c/2l ），叫做「第二泛音」，响度通常比基音低一些

频率为基音3倍的（ 3⋅c/2l ），叫做「第三泛音」，响度通常又比第二泛音低一些

以此类推，频率为 k⋅c/2l 的泛音，就叫做「第 k 泛音」或者「第 k 级泛音」。

音色的形成

不同物体发出的声音，各个级别的泛音会有不同的响度。

例如拍一个西瓜，可能它的第二泛音的响度是基音的80%，敲一块石头，第二泛音的响度是基音的50%，而它们的第三、第四……泛音所占的比例又各不相同。

各个级别的泛音所占的比例，共同形成了这个物体的「音色」。

响度最大的基音，是物体发声时最有代表性、最容易辨识的音调。

而我们的乐器,则是通过改变（c/2l）这个比值,进而改变了音调.弦类乐器通过绷紧程度改变声速c,通过品格改变长度l

和谐的本质

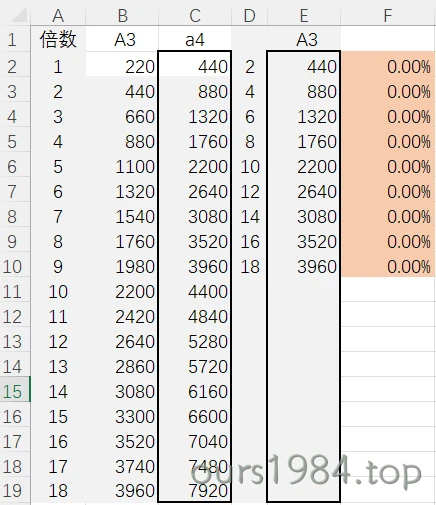
可以想到,一个基音为220hz的泛音列A,混合上一个基音为440hz的泛音列a,a的泛音列被完全地包含在了A的泛音列中。

或者说，弹下A这个音，得到一个泛音列，再同时多弹一个a，居然还是那个泛音列（各个级别泛音的频率没有变，只是响度有变化）。

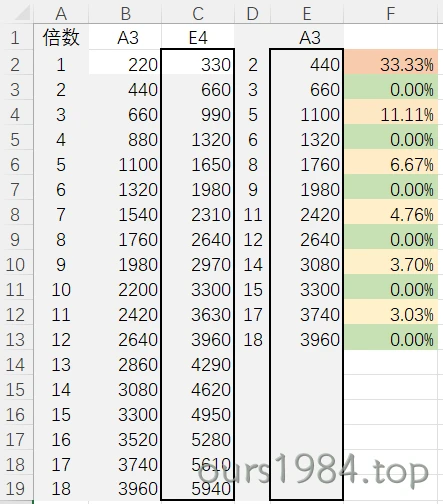
一个基音为220hz的泛音列A,混合上一个基音为330hz的泛音列E,我们会发现他们没有包含关系,但是还是有很多泛音重叠在一起了

比如A的三级泛音,和E的二级泛音,就是一个音.同时,可以发现,E的每一级泛音,有的和A的某一级重叠,有的和A的某一级相差不远

泛音列是人耳能感受到的（但可能需要一些专业的训练才能指认出它们），当A和E两个音依次或者同时弹奏出来时，你会感觉到它们的泛音列密不可分，重合度是如此地高，仿佛这两个音「你中有我，我中有你」，最终变为心灵上的感受——好听！

两个音不同级数的泛音列叠在一起了，这,就是和谐的本质

我们的任务,就是要把这些相互和谐的基音找出来,给他们标上记号,也就是调,然后就可以组合起来作曲啦!

再看一个反面例子，拿230Hz和 A=220Hz 放在一起

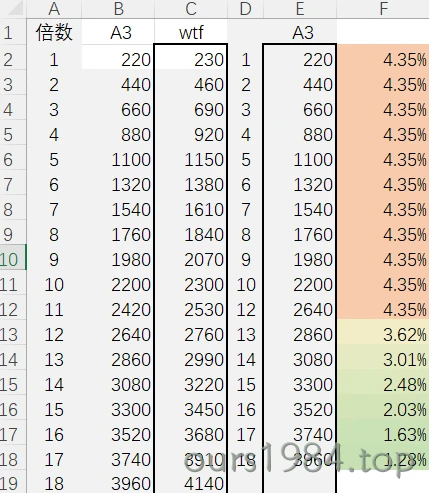
两个音的泛音列之间十分凌乱。反映到听感上就是总觉得这两个音合不到一起去。从频率之差的百分比来看，好像越到高频它们的差异越小，它们的泛音要到第22级、23级才会出现完全重叠，而那个级别的泛音恐怕已经很难被人耳捕捉了。

创造和谐

令其中一个音T1的频率为 f ，另一个音T2的频率是 (n/m)f 。假定这里的n和m已经化为最简分数了，那么：

T1的泛音列与T2的泛音列频率第一次重合是在 n⋅f 处，它是T1的第n级泛音与T2的第m级泛音

第二次重合是在 2n⋅f 处，它是T1的第2n级泛音与T2的第2m级泛音

第三次重合是在 3n⋅f ，它是T1的第3n级泛音与T2的第3m级泛音，以此类推

两个音的频率之比越是一个简单的整数比，亦即n和m数值越小，它们的泛音列中就会有更多的重叠成分，或者说，频率重叠的泛音级别越低（这样它们的响度也比较大，更容易被人耳捕捉到）。

给人的听感就像它们俩天生一对，密不可分。

当然，并不是说频率比比较奇怪的音就一无是处了。比如乐曲中有时会遇到的「小二度」，也就是所谓的「半音」，它的两个音频率之比大概是「1:1.06」，是一个非常远离简单整数比的比例。

这样的音符出现时，往往会给人带来紧张、惊奇的感受，而这可能正是乐曲行进到此处时需要的。

某个时刻要使用中规中矩的稳定音，还是使用刻意营造紧张情绪的不稳定音，就得看作曲的人写到这儿的时候想表现什么情感。

音律

什么是音律呢？音律的概念其实主要就是音和音之间绝对的准确高度和关系，音律分化的律制主要为三种——十二平均律、五度相生律、纯律。

三种律制在实际的应用上各有长处，五度相生律是根据纯五度定律的，因此在音的先后结合上自然协调，适用于单音音乐。

纯律是根据自然三和弦而定律，因此在和弦音的同时结合上纯正而和谐，适用于多声音乐。但随着多声部音乐的发展，转调的频繁，加上键盘乐器在演奏纯律上的困难，因而受到很大限制。

十二平均律在音的先后结合和同时结合上都不是那么纯正自然，但由于它转调方便，在键盘乐器的演奏和制造上有着许多优点，因此近百年来被广泛采用。

十二平均律

十二平均律，又称“十二等程律”，是世界上通用的一组音（八度）分成十二个半音音程的律制，各相邻两律之间的波长之比完全相等。

它是根据对数关系确定音的波长的，然而在八度上，波长的比值却是严格的1:2，所以更完整的说法应该是“八度的十二平均律”。计算波长时，只要对2开12次方根，就可以确定两个半音波长的比值了。

十二平均律是由明朝律学家朱载堉所提出，早于西方五十年出现。他将三分损益法所产生的五度相生律无法还原的问题解决了，由巴赫首先倡导在钢琴上使用的，钢琴上每个半音具有同等地位，因此这种音律在转调频繁的作品中很有优势。

五度相生律是纯律的物理和谐倍数关系，每个调性都会衍生不同的波长差异音阶，为了转调的实用性，才出现十二平均律.平均律的出现虽然解决了转调问题，却也产生另一个和音不够完美的问题。

十二平均律将八度间（倍波长），刻划成平均的十二个音阶，以12个根号2为基数（ 1.059463094 ）为音阶间格，这样完整的十二个平均音阶就可以让12个调性圆满转换，每个音阶都可以吻合应用，钢琴是十二平均律的典型乐器，西洋音乐之父巴哈就以此十二平均律编写了十二种调性的古典乐曲，为十二平均律完整乐曲之始。

五度相生律

它规定五度音的波长之比为2:3，其他音程都由若干个五度产生，根据复合音的第一泛音和第二泛音的纯五度关系，即由某一音开始推一纯五度，产生次一律，再由次一律推一纯五度，产生再次一律，如如此继续相生所定出的音律叫做五度相生律。

五声音阶宫商角徵羽, 按照五度相生律定音，顺序是：宫→徵→商→羽→角。具体说来就是:以一个音「宫」为基础，把它的频率乘以2:3得到音「徵」，再乘以3:4得到「商」……最后再将这些所有音放到一个八度内，得到「宫商角徵羽」这几个音。

显然，这些音都是由一个基础音「宫」频率乘除某个简单整数比得到的，把它们放在一起组成乐曲，听起来就能和谐动听。

按照五度相生律的音高演奏的旋律是最优美的，弦乐器就是典型的按照五度相生律定音的乐器。

五度相生律所订出的七个基本音级间的音高关系，和十二平均律中七个基本音级的音高关系是不同的。虽然EF、BC之间亦为半音，但比十二平均律中的半音要小。

其余相邻两音级之间虽然亦为全音，但比十二平均律中的全音要大。这种音高的差异就是由于定律方法的不同而产生的。

纯律

纯律中任何两个音的波长都成整数比，这种音律源于号角，因为它可以吹出大调音阶中的三和弦(简谱中的1 3 5)，它们的波长之比为15:12:10。

大调音阶中的其它三和弦也可以用这种方法得到，例如简谱中的4 6 1和5 7 2。

这种音律在演奏和声时很有优势，因为波长的整数比可以产生最好的结合。

铜管乐器指法不变时遵循纯律，所以在演奏和声时，要尽可能地使用同样的指法。

由于小调以小三和弦为主(简谱中的6 1 3)，所以波长之比正好与大调相反，为1/10:1/12:1/15，即6:5:4，然而没有一种乐器是按照这种音律定音的。

纯律与五度相生律不同的是，除了规定纯五度音程波长之比为2：3以外，同时规定构成大三度的两个音波长比为4：5，这样制定出各个音高。

纯律的最大优点是因为各音的波长之比都是简单的分数，因而声音最为纯和，提琴族无品弦乐器使用纯律调音。

但纯律转调不方便，转为远关系调时容易失准；而且不能演奏具有较多升降记号的调性，例如升C大、小调。

可视化对比

调式

有了调式之后，才能在固定某一种调式的基础上，来研究这种调式背景下的音程和和弦，这将在后续的文章中展开论述。

大调式

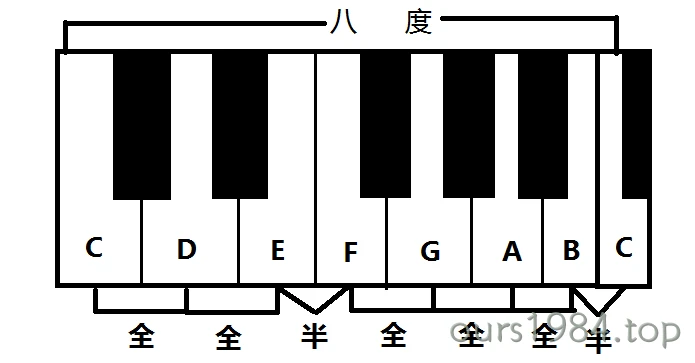
取自然音阶中任何一音为主音，然后按全音、全音、半音、全音、全音、全音、半音的顺序排列而得的调式音阶，即为自然大调式（亦称大音阶）。

这时半音位置在调式音阶的第3与第4、第7与第8音之间，其特点为:主音与其上方三度音、六度音、七度音构成大三度、大六度及大七度音程。

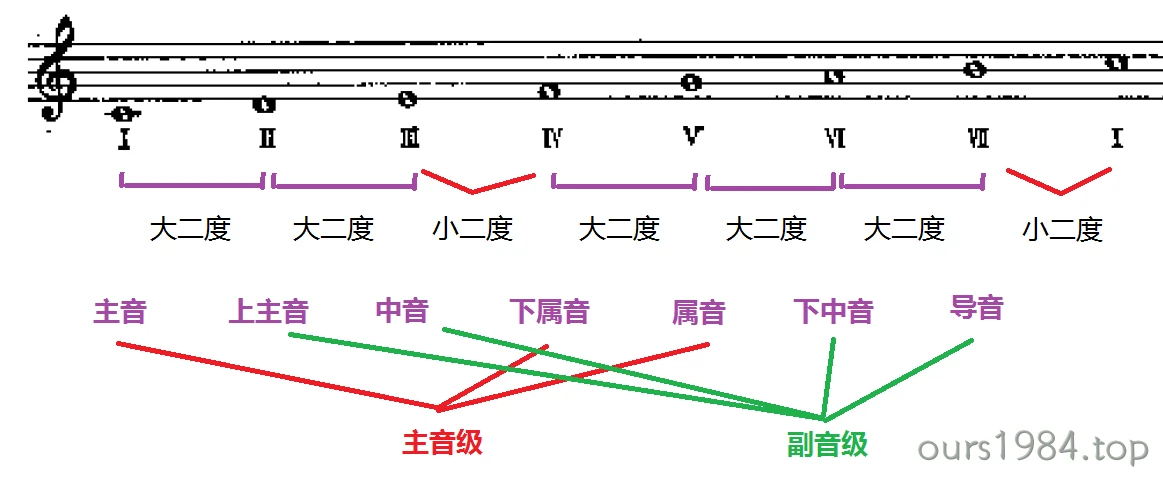
和声大调的话，是将自然大调中的VI级音降半音，其他音级不变。

旋律大调的话，是将自然大调中的VI和VII都降半音，其他音级不变

小调式

按全音、半音、全音、全音、半音、全音、全音的顺序排列，则为自然小调式（亦称小音阶）。

这时半音位置在调式音阶的第2与第3、第5与第6音之间。其特点为：主音与上方三度音、六度音、七度音构成小三度、小六度、小七度音程。

和声小调的话，是将自然小调中的VII级音升半音，其他音级不变。

旋律小调的话，是将自然小调中的VI和VII级音都升半音，其他音级不变。

大小调特点

第Ⅰ级称主音，第Ⅴ级称属音，第Ⅳ级称下属音，三者均为调式骨干音。

第Ⅲ级称中音，第Ⅵ级称下中音，第Ⅱ级称上主音，第Ⅶ级称导音，自然小调第Ⅶ级音称下主音。

自然大调式的主音与其上方三度音、六度音、七度音所构成的音程均为大音程,一般较明亮。

自然小调式的主音与其上方三度音、六度音、七度音所构成的音程均为小音程，一般较暗淡。

和声的与旋律的大、小调式是自然大、小调式在长期的音乐实践中相互渗透的结果，

和声的与旋律的大调式具有一定程度的小调色彩；和声的及旋律的小调式又具有一定程度的大调色彩，

但由于变音的引用，使半音的数目和音程的性质受到改变，所以和声大、小调比自然大、小调增加了不稳定音的倾向及调式的内在紧张度。

五声调式

由按五度相生律生成的五个音组成音阶。将这五个音移到一个八度以内，如下图

在五音中，古人通常以“宫”音作为音阶的第一级音，也是最重要的一个音级，有时借代“五音”。相当于今首调唱名中的do音。“宫”音为五音之主、五音之君，统帅众音。《礼记·乐记》曰：“宫为君、商为臣、角为民……”而以宫音为主音的调，结声构成的调（式）名，便称为宫调。

张炎《词源》亦曰：“十二律吕各有五音，演而为宫为调……黄钟宫（均）：黄钟宫（调式）、黄钟商（调式）、黄钟角（调式）、黄钟变（变徵调式）、黄钟徵（调式）、黄钟羽（调式）、黄钟闰（闰宫调式）。”

五音的第二级音，为“商”音。通常相当于今首调唱名中的re音。古人认为，“商，属金，臣之象”，“臣而和之”。有以商音为主音、结声构成的调（式）名。如唐段安节的《乐府杂录·别乐识五音轮二十八调图》中的“入声商七调”。

“角”为五音之第三级，居“商”之次。通常相当于今首调唱名中的mi音。古人以为，“角属木，民之象”。有以角音为主音、结声构成的调（式）名。如唐段安节的《乐府杂录·别乐识五音轮二十八调图》中的”上声角七调”。在古代的调（式）中，有以角音为调之角调，或有以闰宫为角之角调。

“徵”为五音之第四级，居”角”之次。通常相当于今首调唱名中的sol音。古人以为，“徵属火，事之象”。有以徵音为主音、结声构成的调（式）名。

“羽”为五音之第五级，居”徵”之次。通常相当于今首调唱名中的la音。古人以为，“羽属水，物之象”。有以羽音为主音、结声构成的调（式）名。如唐段安节的《乐府杂录·别乐识五音轮二十八调图》中的“平声羽七调”。

在五声音阶中，分别以不同的各音作为主音时，可构成不同的调式；调式名称是以阶名命名的。比如以第一级音“宫”作为主音时，就称为宫调式，以第二级音“商”作为主音时，就称为商调式，以第三级音“角”作为主音时，就称为角调式，余类推。

调号

表示调号有两种方法：可以直接写“C调”，“C小调”或“Key: C”，“Key: Cm”。

亦可写清楚主音代表哪一个音，例如“1 = C”，就是C大调（大调以1为主音）。“6 = C”就是C小调（小调以6为主音）。“2 = D”就是D多利安调（多利安调以2为主音）。

五线谱有变音记号，简谱同样有变音记号。在简谱中，若需表达升降音，就把符号加在数字1至7的前方，让该音升高或降低。若要把变音记号加在调号跟和弦CDEFGAB七个字母，就须加在它们的后方。

在五线谱中，C小调曲调表达为B，E，A三个音各降低半音。在表达和声C小调的导音时，会把一个还原号放在B♭的音符前面。

而在简谱中用“6 = C”记谱方式表达C小调时，这个导音写作♯5，因为5本身不能被还原，这与五线谱中B已被降半音而需还原的情况不同。

大调	小调	小调	大调
C	Am	Cm	Eb
Db	Bbm	C#m	E
D	Bm	Dm	F
Eb	Cm	D#m	F#
E	C#m	Em	G
F	Dm	Fm	Ab
F#	D#m	F#m	A
G	Em	Gm	Bb
Ab	Fm	G#m	B
A	F#m	Am	C
Bb	Gm	Bbm	Db
B	G#m	Bm	D

和弦

按照三度音程关系或非三度音程关系，三个或以上的音的结合 ，叫做“和弦”。

按三度音程关系构成的和弦，由于各音间保持一定的紧张度，音响协调丰满，并合乎泛音的自然规律，因而被广泛采用。

按非三度音程构成的和弦，虽不像按三度音程构成的和弦那样被广泛采用，但对丰富和声的色彩、建立民族和声语言方面都有着积极的意义，故也不应忽视。

构成和弦的诸音，叫做该和弦的和弦音。在和弦的基本形态中，最下端的一音，叫做“根音”。其余各音均按它们与根音构成的音程关系来命名。

和弦音

根音：它是和弦的一家之主，姓氏命名以它为主。如以C为根音的和弦，无论它后面的组成音是什么，这个和弦的首字母必须是C。例如：C大三和弦、Cm小三和弦、Csus4挂留和弦，等等。

三音：它是和弦的孩子们。由于三音，它分为大三度音与小三度音。所以，有些孩子的性格会像女生一样忧伤与婉约，例如Am小三和弦；有些孩子的性格会像男生一样乐观与奔放，例如F大三和弦。

四音：它是和弦的谜。从三音移动到四音，从而灵动而多变，更像未知的世界，似乎有着一百万种可能。所以，这就是为什么流行歌曲，常喜欢在D和弦后面接上Dsus4的原因之一。

五音：它是和弦的妈妈。正所谓，一山不容二虎，除非一公一母。所以，它会追随根音的属性走起，两者相处极为和谐。所以任何一个旋律音，如果加上五音就可以变成和弦。例如：C和弦加上五音，变成C5和弦，也就是摇滚常用的强力和弦。也许，这就是为什么女生也爱摇滚的原因吧！

七音：它是和弦的新星。当五音被忽略掉，三音和七音会成为新晋明星。所以，当我们只要把三音和七音弹出来，属性立马就会彰显，例如属七和弦G7（1-3-5-b7)。

当我们了解和弦的性质之后，你就是时候学习和弦各音的构成情况了。

三和弦

由三个音按照三度关系叠置起来的和弦，叫做三和弦。三和弦各音由下而上称为根音、三音、五音，分别以1、3、5标记。

和弦种类	根音	三度音	五度音	标记	示例
大三和弦	根音	大三度	纯五度	Major、M、省略	C
小三和弦	根音	小三度	纯五度	minor、m、-	Cm
增三和弦	根音	大三度	增五度	Augment、aug、+	Caug
减三和弦	根音	小三度	减五度	diminish、dim、°	Cdim

七和弦

由四个音按照三度关系叠置起来的和弦，叫做七和弦。七和弦各音由下而上称为根音、三音、五音、七音，分别以1、3、5、7标记。

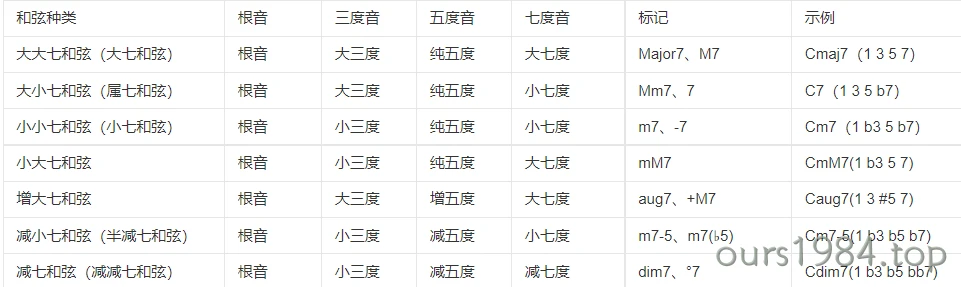
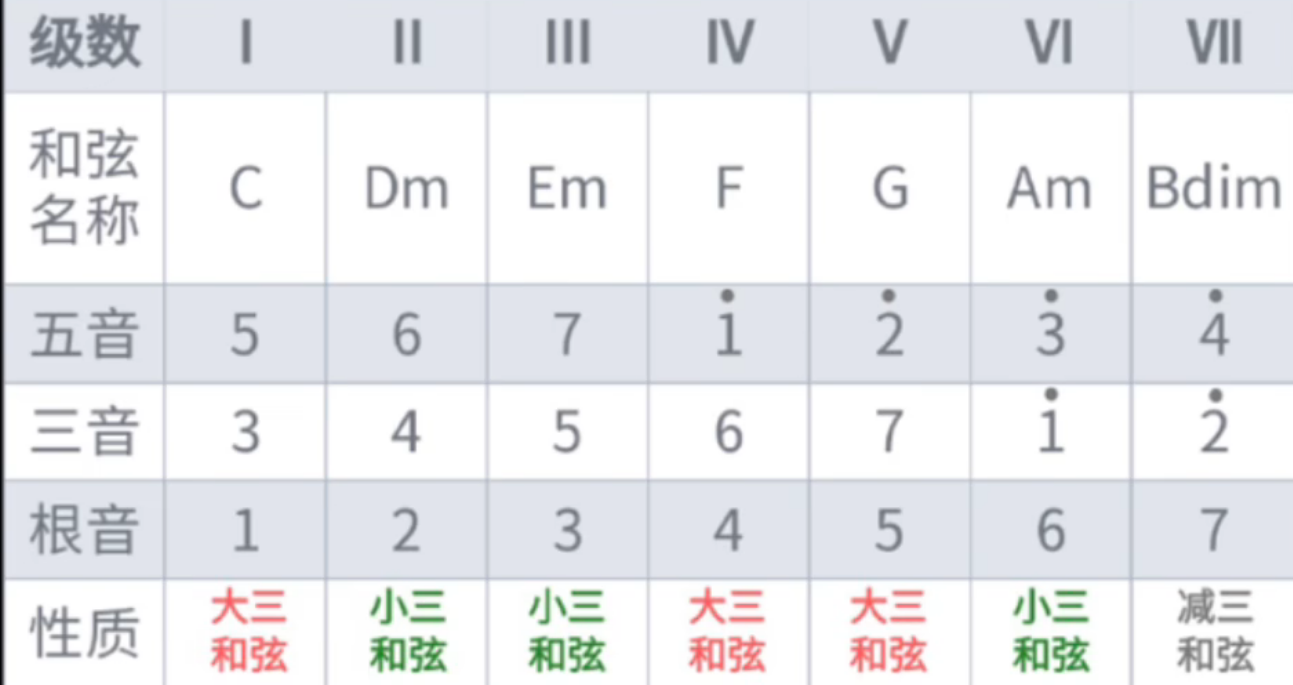
大调级数

吉他转调表

尤克里里转调表