浅出理解非均匀有理B样条

你所熟知的曲线方程

在CAD中，设计师需要设计出各种各样的曲线；数学中，曲线是通过各种各样的方程表示的！比如一条通过点A(0,0)、B(1,1)的直线可以表示为：\(y=x\) 或者用参数方程表示： \(P(u) = (1-u)A+tB\)

再比如一个通过原点(1,2)、半径为2的圆可以表示为：$ (x-1)^2 + (y-2)^2 = 4$

或者用参数方程表示：\(x = 2cos(u)+1 ;y = 2sin(u)+2\)

上面举例的是两种很简单的曲线，对于更复杂的曲线可以用更复杂的方程来表示（比如用高次多项式）；

如果我们的设计师是一位数学家就好了，他可以根据自己的需要，设计出一个复杂的方程来表示自己想要的一条优美的曲线，但是事与愿违，设计师们往往想通过一种直观的方式来设计曲线，而不是利用方程。

因此，诸位科学家和工程师设计出了Bezier曲线、B样条和NURBS

贝塞尔B

下面是一个有四个控制点的Bezier曲线

可以通过改变一个控制点的位置来改变曲线的形状，比如将上图曲线中左边第二个控制点往上移，就可以得到下面的曲线

可以看到，这种曲线生成方式比较直观和灵活，我只需要放置控制点，然后调整控制点的位置来得到想要的曲线，这就避免了和复杂的数学方程打交道，岂不快哉？

有理B

有理函数是两个多项式之比。因此，有理样条（rational spline）是两个样条函数之比。例如，有理B样条曲线可以使用向量描述为 \[ P(u)=\frac{\sum_{k=0}^{n}w_kp_kB_{k,d}(u)} {\sum_{k=0}^{n}w_kB_{k,d}(u)} ,u_{min}\leq u\leq u_{max} ,2\leq d\leq n+1 \] 其中，\(p_k\)是输入的一组n+1个控制点，参数\(w_k\)是控制点的加权因子，值越大，曲线越靠近该控制点\(p_k\)。当所有加权因子都设为1时，得到标B样条曲线

非均匀有理B

通常，图像设计软件包使用非均匀节点向量表达式来构造有理B样条，这些样条称为非均匀有理样条(Non-Uniform Rational B-Splines， NURBS)。 构造有理B样条表达式与构造非有理表达式有相同的步骤。给定控制点集、多项式次数、加权因子、节点向量，使用递归关系即可获得混合函数。

各有千秋的B

Bezier曲线、B样条和NURBS都是根据控制点来生成曲线的，那么他们有什么区别了？简单来说，就是:

• Bezier曲线中的每个控制点都会影响整个曲线的形状
• B样条中的控制点只会影响整个曲线的一部分，显然B样条提供了更多的灵活性
• Bezier和B样条都是多项式参数曲线，不能表示一些基本的曲线，比如圆
• 所以引入了NURBS，即非均匀有理B样条来解决这个问题；

Bezier曲线只是B样条的一个特例而已，而B样条又是NURBS的一个特例，它们的关系可以图示为：

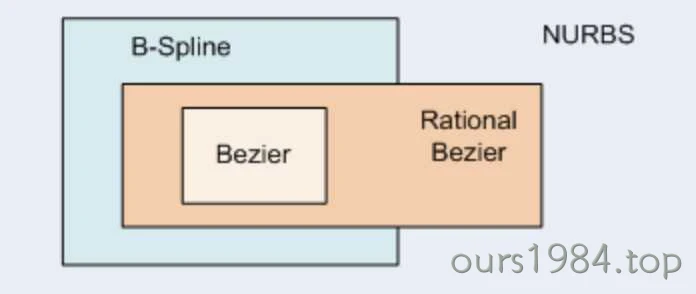
B样条克服了Bezier曲线的一些缺点，Bezier曲线的每个控制点对整条曲线都有影响，也就是说，改变一个控制点的位置，整条曲线的形状都会发生变化，而B样条中的每个控制点只会影响曲线的一段参数范围，从而实现了局部修改